[통계] 선형회귀와 알고리즘

(출처) edwith 모두를 위한 딥러닝, Sung, Kim

 

 

H(x) = W * x (b = 0)

비용함수도 간단하게 표현 가능

 

---

▣ 비용함수의 정의에 따라, 

• W = 1, cost(W) = 1/3 *{(1*1-1)^2 + (2*1-2)^2 + (3*1-3)^2} = 0
• W = 0, cost(W) = 1/3 *{(0*1-1)^2 + (0*2-2)^2 + (0*3-3)^2} = 14/3 =4.67
• W = 2, cost(W) = 1/3 *{(2*1-1)^2 + (2*2-2)^2 + (2*3-3)^2} = 14/3 =4.67

 

---

cost가 최소화되는 점을 찾는 것이 목표이므로 이를 만족하는 값인 W = 1을  기계적으로 찾아냄

---

Gradient descent algorithm 

: 경사를 따라 내려가는 알고리즘

• 비용함수, 머신러닝 최소화 문제에 사용
• W,b의 함수에 적용시켜 최소값을 산출
• 다수의 값을 포함하는 Cost function도 최소화 가능

☞ 경사도가 더 낮은 지점을 향해 이동하며 가장 flat한 지점에 도달할 때까지 아래로 움직임

 

 

How it works?

• Any point에서 시작 → W 이동 → cost 감소 → 최소값까지 반복 
• 어느 점에서 시작하든 최소점에 도달함

 

 

Formal definition

: 경사도에 해당하는 기울기 구하는데 사용되는 미분공식

수식을 간단하게 하기 위해 기존 비용함수 공식을 2로 나눠줌 

 

⊙ a = learning let (상수)

☞ 기울기가 양수이면 W값을 줄여 최소화, 기울기가 음수이면 W값을 늘려 최소화

 

---

비용 함수 미분 과정 

• 알고리즘 반복적 시행으로 최소값 산출
• 미분 계산기(Derivative Calculator) 활용
• 선형회귀의 핵심인 학습과정을 통한 모델 생성

 

---

Convex function

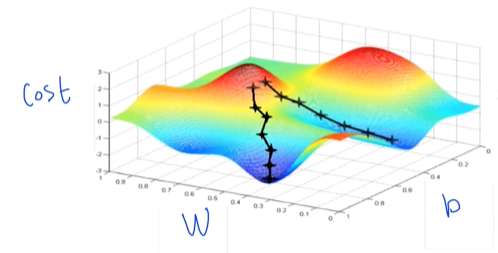
☞ 시작점에 따라 도착점이 달라지면 알고리즘이 제대로 동작하지 않을 것

 

---

convex function

☞ 어느 점에서 시작하든 도착점은 항상 한 곳

• Gradient algorithm이 항상 답을 찾음
• Cost function이 모양이 convex한 지를 확인해야 하는 이유

---

 

I'm a Senior Student in Data Science ! 

데이터 사이언스를 공부하고 있는 4학년 학부생의 TIL 블로그입니다. 게시글이 도움 되셨다면 구독과 좋아요 :)