
↓↓↓ 아래는 내 리트코드 계정 ↓↓↓
Jiwon Lee - LeetCode Profile
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
문제 설명
There are n cities connected by some number of flights. You are given an array flights where flights[i] = [fromi, toi, pricei] indicates that there is a flight from city fromi to city toi with cost pricei.
You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.
입출력 예
Example 1:
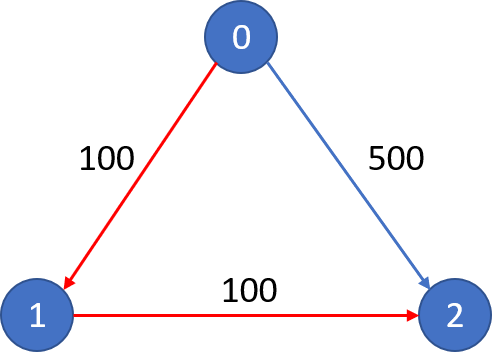
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1 Output: 200 Explanation: The graph is shown. The cheapest price from city 0 to city 2 with at most 1 stop costs 200, as marked red in the picture.
Example 2:
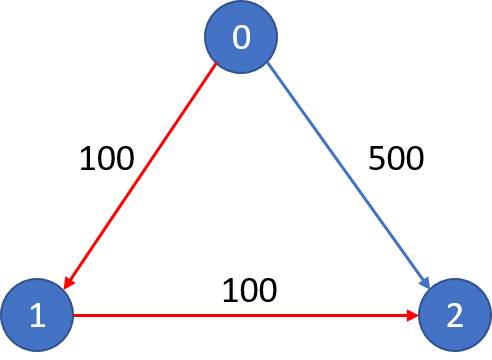
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0 Output: 500 Explanation: The graph is shown. The cheapest price from city 0 to city 2 with at most 0 stop costs 500, as marked blue in the picture.
Constraints
- 1 <= n <= 100
- 0 <= flights.length <= (n * (n - 1) / 2)
- flights[i].length == 3
- 0 <= fromi, toi < n
- fromi != toi
- 1 <= pricei <= 104
- There will not be any multiple flights between two cities.
- 0 <= src, dst, k < n
- src != dst
Code
def findCheapestPrice(self, n, flights, src, dst, K):
graph = collections.defaultdict(list)
for u, v, w in flights:
graph[u].append((v, w))
k = 0
Q = [(0, src, K)] # 비용, 시작노드, 경유지 수로 이루어진 Q 생성
while Q:
price, node, k = heapq.heappop(Q) # 초기값 (0, 시작노드, 0)
if node == dst: # 도착지에 도착했을 때
return price
if k >= 0: # 경유가능한 최대 개수부터 1개씩 줄이는 방식
for v, w in graph[node]:
alt = price + w
heqpq.heappush(Q, (alt, v, k - 1))
return -1 # 모두 경유할 수 없는 경우
이전에 풀었던 네트워크 딜레이 타임 문제와 동일한 유형. 추가되는 제약은 경유지의 개수가 K개로 제한되어 있다는 것이다. 따라서, 나머지 코드들은 같은 방식으로 작성하고, if문을 통해 경유 가능 개수를 넘지 않도록 해준다. (ex. K = 2, if문은 k = 2 -> 1 -> 0으로 총 3번 이동이 가능하다; 경유지 2개 거침) 마지막에는 조건 K 이내에 도착지에 도달하지 못하는 경우 -1을 return하도록 한다. 이전 문제와 달리, 총 거리와 거쳐간 노드에 대한 정보는 저장할 필요가 없으므로 지정해주지 않았다.

I'm a Senior Student in Data Science !
데이터 사이언스를 공부하고 있는 학부생의 TIL 블로그입니다. 게시글이 도움 되셨다면 구독과 좋아요 :)
'Programming > #Algorithm' 카테고리의 다른 글
| [알고리즘] Leetcode #543 이진 트리의 직경 (Python) (0) | 2021.05.13 |
|---|---|
| [알고리즘] Leetcode #104 이진 트리의 최대 깊이 (Python) (0) | 2021.05.12 |
| [알고리즘] Leetcode #743 네트워크 딜레이 타임 (Python) (0) | 2021.05.11 |
| [알고리즘] Leetcode #15 세 수의 합 (Python) (0) | 2021.02.13 |
| [알고리즘] Leetcode #49 그룹 애너그램 (Python) (0) | 2021.02.12 |



