
↓↓↓ 아래는 내 리트코드 계정 ↓↓↓
Jiwon Lee - LeetCode Profile
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
문제 설명
Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree.
입출력 예
Example 1:
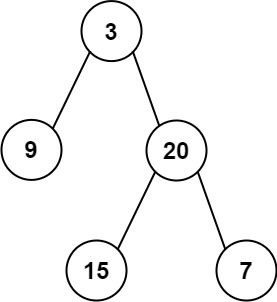
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] Output: [3,9,20,null,null,15,7]
Example 2:
Input: preorder = [-1], inorder = [-1] Output: [-1]
Constraints
- 1 <= preorder.length <= 3000
- inorder.length == preorder.length
- -3000 <= preorder[i], inorder[i] <= 3000
- preorder and inorder consist of unique values.
- Each value of inorder also appears in preorder.
- preorder is guaranteed to be the preorder traversal of the tree.
- inorder is guaranteed to be the inorder traversal of the tree.
Code
def buildTree(self, preorder, inorder):
if inorder:
# 전위 순회 결과는 중위 순회 분할의 인덱스
index = inorder.index(preorder.pop(0)) # pop(0)는 왼쪽부터 pop (Queue)
# 전위 순회의 첫 번째 노드를 트리의 분할 기점 노드로 잡아 left, right구성
node = TreeNode(inorder[index])
node.left = self.buildTree(preorder, inorder[0:index])
node.right = self.buildTree(preorder, inorder[index + 1:])
return node전위, 중위, 후위 순회 중 2가지만 주어지면 트리를 구성할 수 있다. 이 문제는 전위, 중위 순회를 리스트로 주어주고, 트리를 복구하는 문제이다. 이때, 전위 순회의 첫 값을 기준으로 중위 순회에서의 왼쪽, 오른쪽 노드들이 분할된다는 아이디어를 활용할 수 있다. 이를 위해 preorder 리스트의 왼쪽 값부터 pop(0)로 값을 뽑아와 inorder의 기준 인덱스로 사용한다. 이후 인덱스를 기점으로 왼쪽 값들은 왼쪽 노드에, 오른쪽 값들은 오른쪽 노드에 할당하는 작업을 재귀구조로 구현해 트리를 구성해간다.
'Programming > #Algorithm' 카테고리의 다른 글
| [알고리즘] Leetcode #336 팰린드롬 페어 (Python) (0) | 2021.07.06 |
|---|---|
| [알고리즘] Leetcode #215 배열의 K번째 큰 요소 (Python) (0) | 2021.07.03 |
| [알고리즘] Leetcode #783 이진 탐색 트리(BST) 노드 간 최소 거리 (Python) (0) | 2021.06.28 |
| [알고리즘] Leetcode #938 이진 탐색 트리(BST) 합의 범위 (Python) (0) | 2021.06.27 |
| [알고리즘] Leetcode #1038 이진탐색트리(BST)를 더 큰 수의 합계 트리로 (Python) (0) | 2021.06.26 |



