
↓↓↓ 아래는 내 리트코드 계정 ↓↓↓
Jiwon Lee - LeetCode Profile
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
문제 설명
Given the root node of a binary search tree and two integers low and high, return the sum of values of all nodes with a value in the inclusive range [low, high].
입출력 예
Example 1:
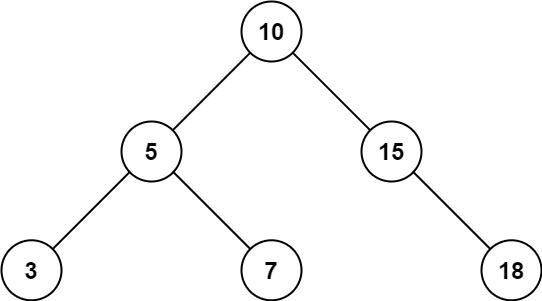
Input: root = [10,5,15,3,7,null,18], low = 7, high = 15 Output: 32 Explanation: Nodes 7, 10, and 15 are in the range [7, 15]. 7 + 10 + 15 = 32.
Example 2:
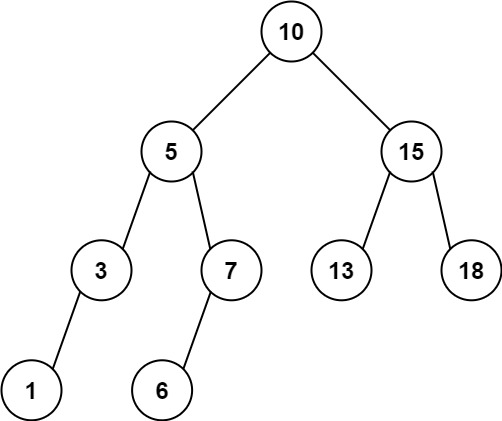
Input: root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10 Output: 23 Explanation: Nodes 6, 7, and 10 are in the range [6, 10]. 6 + 7 + 10 = 23.
Constraints
- The number of nodes in the tree is in the range [1, 2 * 104].
- 1 <= Node.val <= 105
- 1 <= low <= high <= 105
- All Node.val are unique.
Code
# DFS 가지치기로 필요한 노드 탐색 (최적화)
def rangeSumBST(self, root, L, R):
def dfs(node: TreeNode):
if not node:
return 0
if node.val < L: # 최솟값보다 작으면 오른쪽,
return dfs(node.right)
elif node.val > R: # 최댓값보다 크면 왼쪽으로
return dfs(node.left)
return node.val + dfs(node.left) + dfs(node.right)계속해서 다루는 BST! dfs 함수에서는 루트(트리노드)의 첫 번째 값부터 문제에서 주어진 L, R과 비교하며 최솟값보다 작은 값들과 최댓값보다 큰 값들을 pruning해가며 DFS한다. 이렇게 하면 모든 노드를 다 돌면서 하나하나 체크하는 것에 비해 효율이 좋다. 마지막으로, 위에서 정의한 dfs함수에 현재노드의 왼쪽, 오른쪽 노드값을 대입하며 맨 아래 노드에서부터 조건에 맞는 value를 차례로 더해 return한다.
'Programming > #Algorithm' 카테고리의 다른 글
| [알고리즘] Leetcode #105 전위, 중위 순회 결과로 이진 트리 구축(Python) (0) | 2021.07.01 |
|---|---|
| [알고리즘] Leetcode #783 이진 탐색 트리(BST) 노드 간 최소 거리 (Python) (0) | 2021.06.28 |
| [알고리즘] Leetcode #1038 이진탐색트리(BST)를 더 큰 수의 합계 트리로 (Python) (0) | 2021.06.26 |
| [알고리즘] Leetcode #108 정렬된 배열의 이진 탐색 트리 변환 (Python) (0) | 2021.06.25 |
| [알고리즘] Leetcode #310 최소 높이 트리 (Python) (0) | 2021.06.24 |



