
↓↓↓ 아래는 내 리트코드 계정 ↓↓↓
Jiwon Lee - LeetCode Profile
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
문제 설명
Given the root of a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus sum of all keys greater than the original key in BST.
As a reminder, a binary search tree is a tree that satisfies these constraints:
- The left subtree of a node contains only nodes with keys less than the node's key.
- The right subtree of a node contains only nodes with keys greater than the node's key.
- Both the left and right subtrees must also be binary search trees.
Note: This question is the same as 538: https://leetcode.com/problems/convert-bst-to-greater-tree/
입출력 예
Example 1:
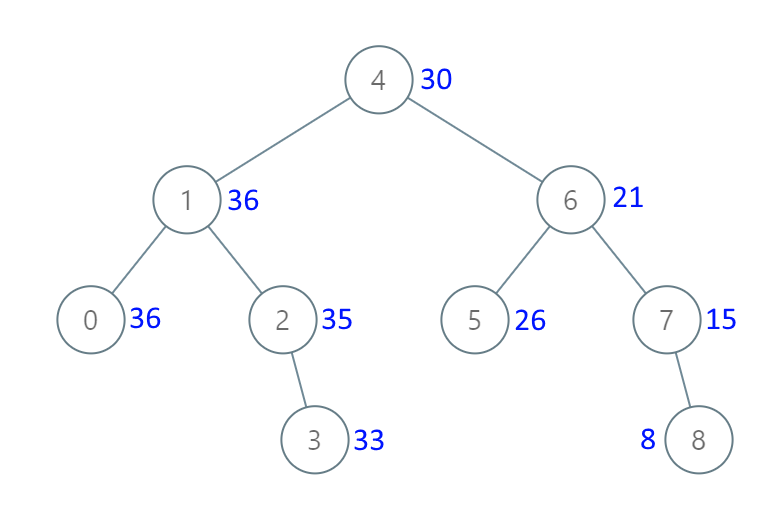
Input: root = [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8] Output: [30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
Example 2: Input: root = [0,null,1] Output: [1,null,1]
Example 3: Input: root = [1,0,2] Output: [3,3,2]
Example 4: Input: root = [3,2,4,1] Output: [7,9,4,10]
Constraints
- The number of nodes in the tree is in the range [1, 100].
- 0 <= Node.val <= 100
- All the values in the tree are unique.
- root is guaranteed to be a valid binary search tree.
Code
class Solution:
val: int = 0 # 클래스 멤버 변수 초기화
def bstToGst(self, root: TreeNode) -> TreeNode:
# 중회 순회 노드 값 누적
if root:
self.bstToGst(root.right)
self.val += root.val # 누적된 값
root.val = self.val # 현재 노드
self.bstToGst(root.left)
return root입력 값이 BST로 주어지기 때문에 특정 노드를 중심으로 오른쪽에는 더 큰 값이, 왼쪽에는 더 작은 값이 할당된다. 이에 따라 문제의 지시처럼 현재노드보다 큰 값들을 모두 더한 값으로 노드 값을 변경하려면 중위순회를 따라 돌면서 (중심-오른쪽-왼쪽) 0으로 초기화한 self.val에 노드의 값을 누적해 더해준다. 예를 들어, 4에는 4보다 큰 4+ 5+6+7+8 = 30이 할당된다.
'Programming > #Algorithm' 카테고리의 다른 글
| [알고리즘] Leetcode #783 이진 탐색 트리(BST) 노드 간 최소 거리 (Python) (0) | 2021.06.28 |
|---|---|
| [알고리즘] Leetcode #938 이진 탐색 트리(BST) 합의 범위 (Python) (0) | 2021.06.27 |
| [알고리즘] Leetcode #108 정렬된 배열의 이진 탐색 트리 변환 (Python) (0) | 2021.06.25 |
| [알고리즘] Leetcode #310 최소 높이 트리 (Python) (0) | 2021.06.24 |
| [알고리즘] Leetcode #110 균형 이진 트리 (Python) (0) | 2021.05.27 |



